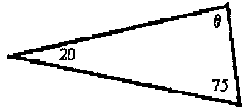Exam Writing Strategies

You may find the following suggestions helpful to your preparation and writing of exams:

Allocate your time (example is for a midterm)

You have 90 minutes to obtain 45 marks - this works out to 2 minutes per mark.

Therefore, you should plan to spend no more than 30 minutes on Part A and about 20 minutes on each of the three Part B questions. If you want, you can factor in some review time by allocating about 10 minutes for review, and dividing 80 minutes by 45 marks to obtain about 1.75 minutes per mark (26 minutes for Part A and 17 minutes for each Part B question).

'Bank' your marks

You don't have to answer the exam questions from front to back. Remember that the Part B solutions are awarded partial marks for correct work. Review the Part B questions first - if you find one that you know you can do easily, do it! Even if you make a small mistake, these are 'marks in the bank'! If you work through the questions from easiest to most difficult then by the end of the exam you will be working on questions that you may not have been able to answer anyway - and you won't have wasted time on these questions earlier.

Prepare as if the exam were an athletic/music/dance competition

Many of you are athletes (past or present), or have competed in music festivals or dance competitions, etc. Many of your pre-competition strategies can be applied to writing exams:

avoid staying up late the night before the exam
eat a nutritious breakfast, lunch, and dinner the day of the exam
bring a bottle of water to the exam
avoid cramming in the hours before the exam, try going for a walk to clear your mind of negative thoughts
make use of any mental training that you may have received - meditation, visualization, relaxation, etc.
take a few calming deep breaths before opening the exam booklet

Hopefully you will find some of these suggestions helpful.

Physics 111 Algebra Review

Fractions

A fraction's value is unchanged if the numerator and denominator are each multiplied or divided by the same quantity.

Thus the following relations hold:

and therefore,

Exponents

Raising a number y to an exponent n (the nth power) means that y is multiplied by itself n times.

e.g.

y² = y × y

Note that

y² × y³ = (y × y) × (y × y × y) = y⁵

y^m × yⁿ = y^m+n

and

(y²)³ = (y × y) × (y × y) × (y × y) = y⁶

(y^m)ⁿ = y^m×n

Exponents need not be integers, they can be fractions, less than 1, negative, ... A negative exponent denotes the reciprocal of the number with positive exponent:

e.g.

Note that:

Logarithms

Any number y can be written as another number A raised to an exponent x. Neither A nor x need be integers.

i.e.

y = A^x

The exponent x is called the logarithm of y to the base A and is written as:

x = log_Ay

i.e.

log_A(y) = x means A^x = y

There are two frequently-used bases for logarithms:

Base 10 (A = 10) gives the common logarithms, denoted log

log(1) = 0	and	log(10) = 1
log(10^x) = x	and	10^{log x} = x

Base e (A = e = 2.71828...)gives the natural logarithms, denoted ln

ln(1) = 0	and	ln(e) = 1
ln(e^x) = x	and	e^{ln x} = x

Logarithm relations:

log(ab) = log(a) + log(b)

log(yⁿ) = n log(y)

Equations

An equation is not changed if the same operation is performed on each side of the equation.

Suppose

A + B = C + D

then

(A + B) + M = (C + D) + M

(A + B) - M = (C + D) - M

(A + B) × M = (C + D) × M

(A + B)ⁿ = (C + D)ⁿ

Also,

AC + BC = C × (A + B) = (A + B) × C

Quadratic Equations

An equation is said to be QUADRATIC in a variable if the variable appears to the first and second powers.

The general form of a quadratic equation:

ax² + bx + c = 0

has the solution:

Linear Equations

The general equation for a straight line is:

y = mx + b

where m is the slope and b is the y-intercept (the y value when x = 0).

The slope can be determined graphically by choosing any two points on the line and using

The y-intercept can either be read directly from the graph or, once the slope is known, calculated by using the line equation:

b = y₁ - mx₁

where (x₁, y₁) is a point on the line.

Math Review Questions

Links to the solutions to these questions are at the bottom of this page.

1.	Determine the UNITS of x in each of the following equations: a) x = (15 m) / (2.0 s) b) x = (3.2 × 10^–19 J)(6.21 × 10^–7 m) / (3.00 × 10⁸ m/s) c) x = [(1.50 kg.m/s²) / (1.00 × 10^–4 kg/m)]^½
2	Express the following numbers to 3 significant figures and use scientific notation: a) 134,000 b) .01936
3	Express the following numbers to 3 significant figures and use decimal notation: a) 2.9987 × 10¹ b) 3.61 × 10^–3
4	Solve each of the following equations for x. Recall that the logarithm of x to base 10, denoted log(x), is the exponent to which 10 must be raised to obtain the value of x. Note that log(x) is the inverse of the function 10^x. log(10^x) = x. a) x = log(100) b) x = 10 log(2) c) 3 = log(x) d) 68.8 = 10 log(x / 20) e) 10^2.5x = 5.62 × 10^–3
5	Solve each of the following equations for x. Recall that the logarithm of x to base e, denoted ln(x), is the exponent to which e must be raised to obtain the value of x. Note that ln(x) is the inverse of the function e^x. log(e^x) = x. a) x = ln(7.389) b) x = e^–2.5 c) x = 1500 e^{–(0.042)(5.3)} d) 2 = e^4x e) 15 = 30 e^–(0.05)x
6	Solve each of the following equations for x: a) a + x = b b) a – x = b – c c) (a + b) / c = d / x d) ax(b – x) = –cx e) 40(x + 21) = 32(15 – x)
7	The final speed, v, of an object initially moving at speed v_o and undergoing uniform acceleration a for a time t is: v = v_o + at A car is moving at a speed of 90 km/h after undergoing a uniform acceleration of 3.0 m/s² for a time of 5.0 seconds. What was the initial speed of the car?
8	Solve each of the following equations for x: a) x² – 4x + 4 = 0 b) 3x² – 2x – 1 = 0 c) 12.0 = 8.61x + 4.90x²
9	The displacement, x, of an object with initial speed v_o undergoing constant acceleration a for an elapsed time t is given by: x = v_ot + ½at² Calculate the time for a ball to hit the ground if it is thrown straight down from a window 15 m above the ground with an initial speed of 20 m/s. The acceleration of the ball is 9.8 m/s².
10	Solve for the values of x and y that satisfy the following pairs of equations: a) 3x + 2y = 7 ; 2x – 5y = 6 b) 0.60x + y – 98 = 0 ; 0.80x – 0.40y – 10 = 0 c) x / y = 0.0924 ; x² / y = 5.54 d) y cos(x) = 15.0 ; y sin(x) = 30.0
11	Determine the slope, y-intercept, and x-intercept for the graph of y versus x that is represented by the linear equation 3x + 2y = 7.
12	Determine the slope, y-intercept, and x-intercept for the graph of y versus x that passes through the two points having (x, y) coordinates of (–1, 6) and (2, –9).
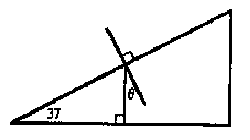
13	Determine the value of the angle in each of the following diagrams: a) b) c)
14	Determine the values of x and in the following diagram. (HINT: Are the two triangles similar?)
15	Write the expressions for the circumference, C, and area enclosed, A, for a circle of radius R.
16	Write the expressions for the perimeter, P, and area enclosed, A, for a rectangle of sides and w.
17	Write the expressions for the surface area, A, and volume, V, of a sphere of radius R.
18	Write the expressions for the surface area, A, and volume, V, of a cube of side
19	Write the expression for the area of intersection, A, of a sphere of radius R and a plane passing through the centre of the sphere. (i.e. Write the expression for the maximum cross-sectional area of a sphere.)
20	Write the expression for the area, A, of a triangle of base b and height h.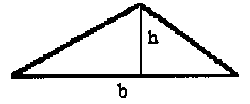
21	Write the expression for the volume, V, of a right circular cylinder of radius R and height h.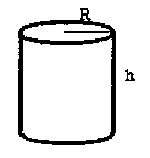
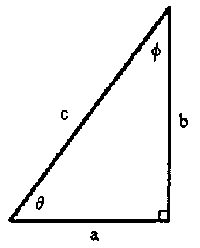
22	With reference to the labelled right triangle, calculate the requested quantities. a) a = 3.5, b = 6.2, c = ?, = ?, = ? b) c = 5.0, = 37°, a = ?, b = ? c) tan = 0.75, = ? d) a = 2.4, = 60°, c = ? e) a = 1.8, c = 2.5, = ?
23	If a person walks a distance x due west and then walks a distance y due north, the straight line distance from the start point, r, is: A person walks away from a cabin a distance of 240 m due west, then turns and walks a distance y due north and ends up a straight line distance of 300 m from the cabin. How far north did the person walk?
24	A person stands 20.0 m in front of a tall building and looks up toward a window. The person's line of sight makes an angle of 55.0° above the horizontal. How far above the person's eyes is the window?
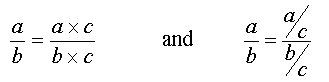
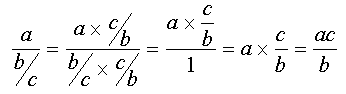
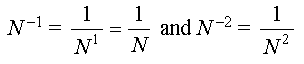
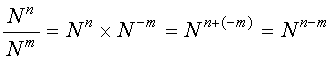
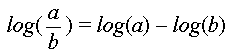
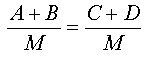
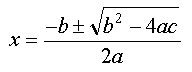
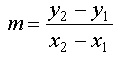
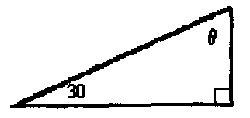25	The three vectors A, B, and C are described as follows: A_x = 6.0, A_y = –8.0 ; B_x = –3.0, B_y = 5.0 ; C makes an angle of 30° with the x axis and its magnitude is 8.0 units. Find the magnitudes and directions of the vectors A and B and the components of vector C. Find the vector E = A – B.