1996/97 Test 1 Parts B & C
To aid you with your exam preparation, the following are the Parts B and C questions from the 1996/97 first midterm. (NOTE: The Part A questions of the 1996/97 first midterm are the questions in the Self-Graded Quiz #1.)
B1. A car is initially at rest. It accelerates uniformly to a speed of 15.0 m/s over a distance of 35.0 m. What is the magnitude of the car's acceleration?
B2. A projectile is fired at an angle of 60.0° above the horizontal with an initial speed of 30.0 m/s. What is the magnitude of the horizontal component of the projectile's displacement at the end of 2.00 s?
B3. A system of two cables supports a ball of weight 150 N as shown. What is the tension in the right-hand cable? 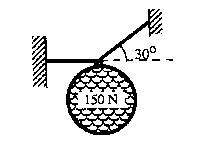
B4. Calculate the speed of an Earth satellite that is in a stable circular orbit of radius 6.90 × 106 m. Mass of the Earth: 5.98 × 1024 kg.
B5. A block of mass 2.00 kg slides, from rest, down the frictionless surface shown. The block starts at a height of 3.00 m above the bottom of the slope. Find the speed of the block at the bottom of the slope.
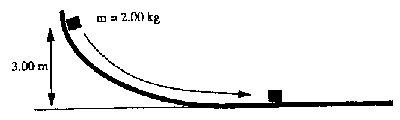
C1. A diver springs from a diving board which is 3.00 m above the water. At the instant she contacts the water, her speed is 8.90 m/s and her trajectory makes an angle of 75.0° with respect to the horizontal surface of the water. Determine her initial velocity, both magnitude and direction. (Provide a sketch and indicate your choice of coordinate system. Specify the direction by the angle from the horizontal.)
C2. A car is initially moving at a speed of 20.0 m/s down a hill that is at an angle of 15.0° with the horizontal. The driver of the car slams on the brakes, causing the wheels to lock and the car skids to a halt. The coefficient of kinetic friction between the tires and the road surface is 0.650. Calculate the distance the car skids before coming to rest.
C3. A crate of mass 6.00 kg is given a shove on a horizontal rough surface so that it has an initial speed of 6.26 m/s. It comes to rest in a distance of 4.00 m from the point where it was shoved.
- Calculate the work done by the force of friction on the crate.
- Using the result from (a), calculate the coefficient of kinetic friction between the crate and the surface.
Solutions:
- View Page 1 (questions B1, B2, B3, B4)
- View Page 2 (question B5)
- View Page 3 (question C1)
- View Page 4 (question C2)
- View Page 5 (question C3)

